ノンパラメトリック検定の検出力

　母集団が正規集団している場合のために開発されたパラメトリックな統計手法は、実際に母集団が正規集団の場合、最も強力な検定であり、比較的計算が簡単な便利な統計手法です。しかし、母集団が正規分布から外れた場合、その限りではなく時には著しく検出力が低くなることすらあります。
　一方、ならべかえ検定に基づくノンパラメトリックな統計手法は、もともと特定の分布の母集団のためのもではないので、母集団の分布の形に影響を受けにくいと考えられます。また正規集団においても、ノンパラ統計がかなり高い検出力を示す場合があります。以下に2群の平均値の比較を例に、母集団の形の影響を見てみましょう。

母集団が正規分布の場合

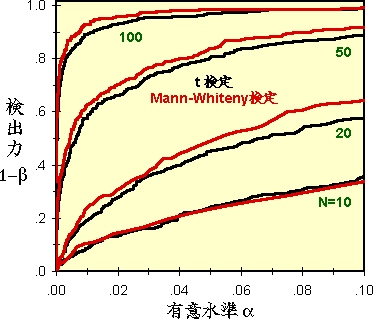
まず右図のような２つの正規集団を用いて、t検定 と Mann-Whiteny検定 の検出力を比較してみましょう。２つの集団からランダムにN個づつ抽出して、検定する過程を300回繰り返しました。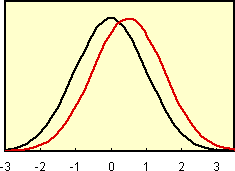

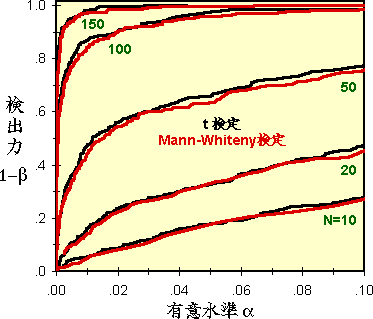	正規集団に特化した t検定 は母集団が正規分布では最も検出力が高いのですが、Mann-Whiteny検定 も t検定 に対して95%の検出力があります。この例でも、どの サンプル数でもわずかに Mann-Whiteny検定 の検出力が低いだけで、殆ど差がないことが分かります。

---

母集団がロジスティック分布の場合

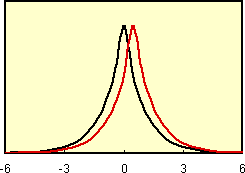
次にパラメトリックな統計の前提とは異なり、母集団がロジスティク分布している場合をみてみましょう。 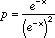で表されるロジスティック分布(右図)は、一見正規分布と酷似しています。事実、正規分布と見分けるためにはかなりのサンプル数が必要になります。ですが実際には、正規分布に比べると平均値から遠ざかっても確率密度(p)が下がりにくい分布です。

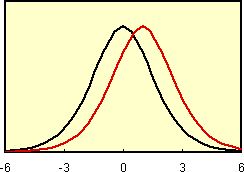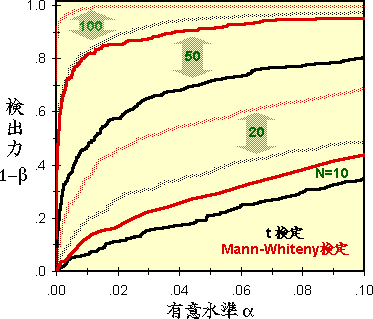
母集団がロジスティック分布の場合、Mann-Whiteny検定 が t検定 より検出力が5%高くなることが解析的に求められています。左図に示した例でも、Mann-Whiteny検定 が t検定 を多少上回っていることが分かります。

---

他の例

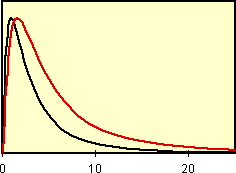
両側指数関数分布	exp(正規変数)
圧倒的に Mann-Whiteny検定 の方が検出力が高いです(t検定 の1.5倍)。※ここでは示していませんが、中央値検定の方が更に有効です(t検定 の2倍)。	対数変換すれば正規分布になるのでt検定が好ましいのですが、変数変換しない場合には Mann-Whiteny検定 の方がかなり検出力が高いです。

まとめ

サンプル数が少なく、母集団の分布が特定できない場合、Mann-Whiteny検定を使っておく方が無難。

サンプル数が非常に多い場合、t検定の検出力もそれほど影響されないので、計算が比較的楽なt検定を用いて構わない。

戻る	・	ソフトウェア

Excel関連のリンク集	日本語入力のお助けリンク集

	廣田 忠雄 @ 山形大学 理学部 生物学科 生物多様性大講座

---