サイコロの細工を見破れるか
| ある主婦が『ごきげんよう』(フジ・月-金PM1:00)を見ていて、そこで使われているサイコロの特定の目がでやすいような気がしてなりませんでした。その目は『今日の当たり目』といって、出ると視聴者にプレゼントが当たるというものです。そこで彼女は、1ヶ月番組を見ながらどの目が幾つ出たかチェックしていました。1日に3-4回サイコロが降られ、22日間カウントした結果、77回のサンプルを得ました。そこで、カイ2乗検定を用いて検定したのですが、5%の有意水準では、普通のサイコロと異なるとは結論できませんでした。 | |
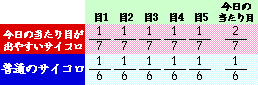
ところが、実際には番組では視聴者へのプレゼントが頻繁に出て番組を盛り上げるように、右図のように『今日の当たり目』が他の目より2倍も出やすくなるように細工をしていました。 では、なぜ彼女の調査では有意差がでなかったのでしょう。 |
 |
|---|---|
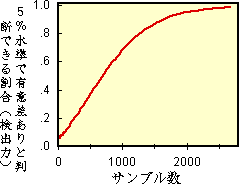 |
実は、上図のようなサイコロと普通のサイコロをカイ2乗検定で見分けるためには、検出力とサンプル数に左図のような関係があるのです。つまり、サンプル数が少ないと、普通のサイコロとの違いを見逃してしまう可能性(第2種の誤り, β)が結構高いのです。今回彼女が1月かけて得た77というサンプル数も、第2種の誤りをする可能性(β)が90%を上回る、かなり不十分なものだったのです。 この例では、第2種の誤り(β)をおこす危険性をほぼ 0 にする (検出力が100%) には、2500回以上もサイコロを振らないといけないのです。 |
差が小さいと見逃しやすい
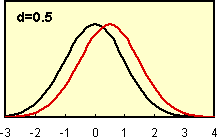
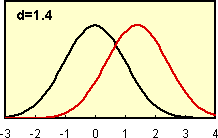
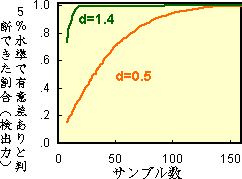
次に下図のような正規分布している集団の平均値の比較する場合の、t検定の検出力をみてみましょう。ここでは、検出しようとしている平均値の差の大きさが、検出力に与える影響を見てみましょう。 左下図は、両分布の平均値の差が小さく(d=0.5)分布がかなり重なっています。一方 右下図は、より平均値の差が大きい(d=1.4)例です。※ d は 平均値の差/分散 です。 |
|
 |  |
|---|---|
実際、上の例の検出力を様々なサンプル数で確かめてみると、d=1.4 の場合にはサンプル数が20になると5%水準でがほぼ100%検出できるのに、d=0.5 では160ものサンプルが必要になります。 このように母集団の平均値の差が、検出力に大きく影響することが分かりました。ですので、検出力を確かめるためにはあからじめ問題となる平均値の差を決めておく必要があります。 |
 |
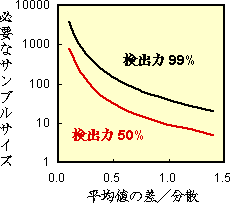 |
この差を決めるには、あなたがその検定をどのような目的で行っているのか立ち返って考えなくてはなりません。例えば、様々な処理がある生物のホルモン濃度に与える影響を調べる場合を想定しましょう。このホルモンはある器官に影響を与えますが、その効果はホルモン濃度がある閾値を越えないと表れません。よって問題となるのは、様々な処理がこの閾値を超えるほどにホルモン濃度を増加させるかであり、それ以下の差はとりあえず問題となりません。そこでこの場合、平常時のホルモン濃度(平均値あるいは信頼区間の上限)と閾値の差を d (=平均値の差/分散) として左図のようなグラフ・数表を参考に必要なサンプル数を求めましょう。 |
|---|
差が無いとを主張するには、有意水準の設定も慎重に
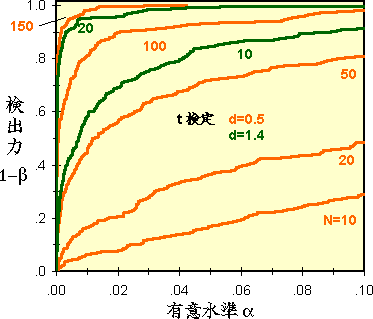
検出力(1-β)は、上で述べたサンプル数(N)と真の差(d)以外に、有意水準(α)によっても変わります(右図)。これは検出力が、棄却率が有意水準以下になる割合であることを考えれば当然といえます。 観察された差が、本当に母集団に差があるために生じたと主張したい場合には、その現象が偶然生じている場合と見分けるために、有意水準を小さくすることで厳しい判断ができます。 だが一方で、母集団に差はなく、観察された差は全くの偶然に生じたと主張したい場合もあります。例としては、特に観察された頻度分布を既知の分布(正規分布・ポワソン分布など)と比較する場合です。この際、サンプル数が非常に大きい場合を除いて、有意水準をいたずらに低く設定してしまうと、検出力が低下して母集団に差がないという結論を導きやすくなってしまいます。そこで有意水準を大きく(時には0.1以上に)設定した方が、かえって厳しい検定になります。 |
 |
| 参考文献 |
|---|
| Cohen, J (1988) Statistical Power Analysis for the Behavioral Sciences 2nd eds., Lawrence Erlbaum Asscociates, Publisher |
| パラメトリックな統計手法を中心に、検出力の概念・算出法を解説した本です。数表がたくさん出ているので、かなり実用的です。 |
| 戻る | ・ | ソフトウェア |
|---|
| Excel関連のリンク集 | 日本語入力のお助けリンク集 |
| 廣田 忠雄 @ 山形大学 理学部 生物学科 生物多様性大講座 |
|---|