母集団がロジスティック分布の場合
  で表されるロジスティク分布(右図)は、一見正規分布と酷似しています。しかし実際には、正規分布に比べると x の絶対値が大きくなっても確率密度(p)が下がりにくい分布です。母集団がロジスティック分布であった場合、t検定よりMann-Whiteny検定の方がわずかに検出力が高くなります。以下のグラフは、ロジスティック分布からランダムにN個のデータを抽出して、その正規性を検定したものです(100回以上抽出)。母集団が正規分布ではないのが既知なので、ちゃんと有意差が検出された割合が検出力となります。 |
| D'Agostino-Pearson検定 | Kolmogorv-Smirnov検定 |
|---|---|
 |
 |
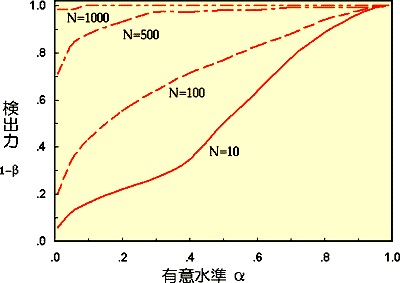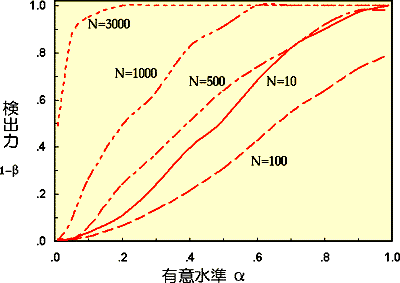| 有意水準を5%以下にする場合、サンプル数(N)が1000以上でないと正規分布と見分けられない場合(第2種の誤り)が、結構あります。 | 有意水準を5%以下にする場合、サンプル数(N)が1000でも、正規分布と見分けられない場合(第2種の誤り)が80%以上あり、N=3000でもまだ完全ではない。 |
母集団が著しく正規分布から解離している場合
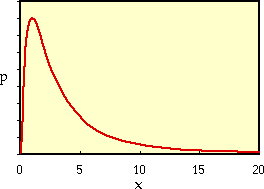 次に、著しく正規分布とは異なる分布で同様のシミュレーションをしてみます。この分布は右図のように著しく左に歪んでいます。ですが、もともと正規分布している集団をeを底にべき乗し作った分布なので、ｘの自然対数をとれば正規分布に戻ります。 |
| D'Agostino-Pearson検定 | Kolmogorv-Smirnov検定 |
|---|---|
 |
 |
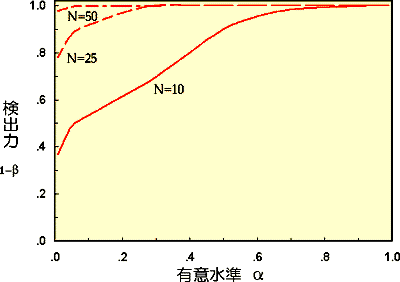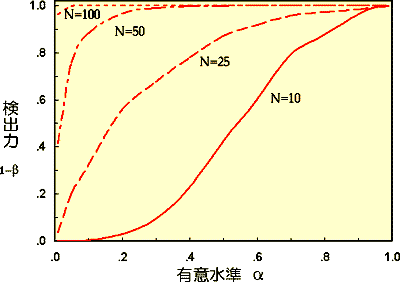| 有意水準を5%以下にする場合、サンプル数(N)が50程度で検出力が100%になります。 | 有意水準を5%以下にする場合、サンプル数(N)が100程度で検出力が100%になります。 |
